Research on R language time series and autoregressive integrated moving average model for predication of receiving and use of anesthetic consumables
-
摘要:目的 运用自回归积分滑动平均模型(ARIMA)建立适合的老年患者特色手术科室耗材领用支出的医学经济学模型，预测麻醉科耗材需求的变化趋势。方法 采用R软件对本院麻醉科2013年1月—2019年12月耗材领用支出数据建立ARIMA模型，将2020年1—12月耗材领用支出的实际值与预测值分别进行比较，评价模型的预测性能。结果 本院麻醉科耗材领用支出在每年2月出现最低值，5月呈现最高峰。建立ARIMA (0，1，1)(0，0，1)[12]模型对麻醉科耗材需求进行预测，ARIMA模型较好地拟合和预测了周期性波动。ARIMA (0，1，1)(0，0，1)[12]模型预测的耗材支出在2020年1—12月会有小幅波动。结论 ARIMA (0，1，1)(0，0，1)[12]模型较好地拟合了麻醉科的耗材需求，有助于优化科室决策支持系统及老年择期手术患者围术期护理管理。
-
关键词:
- 医学经济学 /
- 老年患者 /
- 决策支持系统 /
- 管理 /
- 自回归积分滑动平均模型
Abstract:Objective To establish a suitable medical economics model of receiving and use of specialized surgery consumables in the elderly patient in Department of Anesthesiology by using the autoregressive integrated moving average (ARIMA) model, and to predict the changing trend of the consumables demand in Department of Anesthesiology.Methods R software was used to establish the ARIMA model based on the data of consumables acquisition and expenditure of Anesthesiology Department in authors' hospital from January 2013 to December 2019. The actual value and the predicted value of consumables acquisition and expenditure were compared from January to December 2020, and prediction performance of the model was evaluated.Results The consumption expenditure of Anesthesiology Department in authors' hospital was the lowest in February and the highest in May every year. ARIMA(0, 1, 1)(0, 0, 1)[12] model was established to predict the consumable demand of Anesthesiology Department, and ARIMA model met and predicted the periodic fluctuation well. ARIMA(0, 1, 1)(0, 0, 1)[12] model predicted that the consumption of consumables will fluctuate slightly from January to December in 2020.Conclusion ARIMA(0, 1, 1)(0, 0, 1)[12] model can better fit the needs of consumables in Anesthesiology Department, which is helpful to optimize the department decision support system and perioperative nursing management of elderly patients undergoing elective surgery. -
本院外科手术患者以老年人居多，麻醉科为应对老年手术患者麻醉的特色需求，相应的医用耗材用量更多[1-2]。合理地领用耗材可以在保证使用、提高工作效率的同时减轻库存压力、减少浪费[3]。自回归积分滑动平均模型(ARIMA)是时间序列预测中常用的模型，在医学领域中得到了很好的应用[4]。该模型的原理是滤除数据中的高频噪声，基于线性相关检测局部趋势，预测发展趋势[5]。与经典的最小二乘回归一样，自变量和因变量之间的关系很容易通过模型的假设来理解。该模型可以在一个时间序列中以自动化的方式进行模型选择，从而最大限度地提高预测精度[6]。本研究根据复旦大学附属华东医院麻醉科每月领用耗材支出历史数据建立ARIMA模型，预测当前的发展趋势，以判断过去的耗材领用方式是否合理，预测未来需求的发展趋势，为今后科室医用耗材的领用支出提供理论依据。
1. 材料与方法
1.1 一般资料
收集2013年1月—2019年12月复旦大学附属华东医院麻醉科统计数据库中每月耗材支出数据用于构建ARIMA模型，利用2020年1—12月的数据对模型的预测性能进行评价。
1.2 ARIMA模型
ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括自回归过程(AR)、移动平均过程(MA)、自回归移动平均过程(ARMA)以及ARIMA过程。该模型表示为ARIMA(p, d, q)(P, D, Q)[S], p指自回归的顺序, d指趋势程度的差异, q指移动平均数的顺序, P指周期性自回归滞后, D指周期性差异的程度, Q指周期性移动平均数, S指周期模式的长度[7], 包括时间序列平稳性分析、参数估计、模型检验和模型的预测[8-9]。
1.2.1 时间序列平稳性分析
当拿到一组时间序列，需要对其进行平稳性检验，观测不同时期序列各项的相关关系。对数变换和差分是稳定时间序列的首选方法[10], 根据观测序列的自相关图和偏自相关图判断序列平稳性。另外，可根据增广迪基-福勒检验(ADF)估计时间序列是否平稳[11]。
1.2.2 参数估计
采用自相关函数(ACF)和偏自相关(PACF)图表估计ARIMA模型的参数。本研究采用自动识别和人工估计相结合的方法。首先采用R软件中的"auto. arima()"命令自动识别模型参数，然后用ACF和PACF来确认p、q和P、Q。
1.2.3 模型评估
采用Box-Jenkibs Q检验对p、q及P、Q变阶模型进行检验[12]。所有的模型行残差检验(显示为白噪声序列)，使用Akaike信息标准(AIC)比较，以找到最好的模型。本研究评价了ARIMA模型的拟合能力和预测能力。
1.3 数据处理与分析
使用Excel 2016构建麻醉科耗材领用支出数据库，使用R3.5.1软件开发ARIMA模型，显著性水平为0.05。
2. 结果
2.1 麻醉科耗材领用支出的趋势
根据观测的时序序列图显示, 2013—2014年支出呈下降趋势，此后呈逐年上升趋势; 在每年2月呈现最低的支出，随后迅速上升，说明该序列不平稳(图 1A)。本研究通过1次Log平滑和1次差分使序列图比较平稳(图 1B)。
2.2 平稳性检测
经过趋势差分(d=1)和周期性差分(D=1)消除数值不稳定性。根据自相关图和偏相关图可以直观地感受自相关系数始终在0周围波动，应判定该序列为平稳时间序列(图 2)。采用ADF检验对差分后的序列进行平稳性检验，结果显示P=0.02, 说明序列为平稳序列。
在1个周期内, lag1后ACF下降到0, 偏自相关函数(PACF)则在lag0降到0, 因此p=0, q=1。在4个周期中, ACF在第1个周期结束时下降(lag12), 但接近于0, 因此Q=1或2。lag12时PACF为0, 故P=0。为了使结果更加可靠，对P=1进行了检验。D=1, d=0。此外，利用R3.5.1软件中的"auto. arima()"自动识别参数，残差检验结果和赤池信息量准则(AIC)值见表 1。这些模型均满足残差时间序列的白噪声要求，故对AIC值进行比较。自动识别的模型ARIMA(0, 1, 1)(0, 0, 1)[12]的AIC最低，被选为本研究的最佳ARIMA模型。
表 1 ARIMA模型极大似然方法检验和AICARIMA模型 ma s. e. sma s. e log likelihood AIC ARIMA(0, 1, 1)(0, 0, 1)[12] -0.811 2 0.062 7 0.335 7 0.146 6 -27.08 60.17 ARIMA(1, 1, 0)(1, 0, 0)[12] -0.641 8 0.094 3 0.200 2 0.200 2 -30.26 66.53 ARIMA(0, 1, 1)(1, 0, 1)[12] -0.806 7 0.063 6 0.530 5 0.374 1 -26.94 61.88 ARIMA(1, 1, 1)(0, 0, 1)[12] -0.747 4 0.106 9 0.361 2 0.147 4 -26.18 60.36 ARIMA(0, 1, 2)(0, 0, 1)[12] -0.912 8 0.116 1 0.354 5 0.146 6 -26.45 60.90 2.3 预测效果
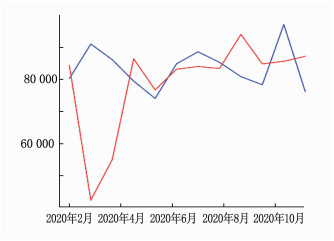
模型建立后，以2020年1—12月本院麻醉科耗材领用实际支出数据作为验证集，将预测值与实际值进行比较分析, ARIMA模型较好地拟合和预测了周期性波动，见图 3、4。ARIMA(0, 1, 1)(0, 0, 1)[12]模型预测的耗材支出在2020年1—12月会有小幅波动。
3. 讨论
本院2018—2020年外科手术患者中，年龄≥65岁者约占50%, 择期手术多为恶性肿瘤等较大创伤手术，老年患者常伴有复杂的合并症，为了确保开展高风险手术的安全性，作者发现单价较高的麻醉耗材消耗较大。虽然昂贵的耗材、进阶的技术和监护增加了麻醉的费用，但可以减少围术期严重并发症的发生，进而降低了最终整体的医疗消耗，使老年择期手术患者获得更好的预后。研究[13]表明，老年髋部骨折患者早期实施髂筋膜间隙阻滞可减少阿片类药物的使用，减轻疼痛和缩短住院时间。
结构化建模基础和可接受的预测性能使得ARIMA模型在时间序列预测中得到了广泛的应用[14]。从2013—2019年数据来看，本院麻醉科耗材领用支出逐年上升，这一方面源于手术麻醉数量的增多，另一方面源于以老年患者为主的麻醉对质控安全及新技术的需求增强。目前，在预测中常见的应用有线性回归、人工神经网络和灰色模型等多种数学方法[15]。线性回归采用了最小二乘法计算，结果易于理解，计算不复杂，但是对非线性数据拟合不好[16]。神经网络通常需要更多的数据，至少需要数千数百万个标记样本，相比传统算法的计算代价更高[17]。灰色模型在数据少时也能大致预测出结果，但不适用于数据之间波动性和随机性较大的预测，不能满足一个简单的函数关系[18]。本研究运用R语言时间序列和ARIMA预测模型，验证ARIMA(0, 1, 1)(0, 0, 1)[12]模型对本院麻醉科耗材领用支出的预测性能最佳。这个模型一旦被识别后，就可以从时间序列的过去值及现在值来预测未来值[19]。本院麻醉科耗材领用支出数据显示, 2018年7月—2018年10月复旦大学附属华东医院麻醉科耗材领用支出将略有下降，随后将大幅上升，这与通常情况类似。2018年11月(cost=1 140 446.00) 的耗材领用支出低于2017年11月(cost=1 711 022.10), 但高于2016年11月(cost=665 145.38)和2015年11月(cost=280 804.6)。这一结果表明，在2018年11月之前应增加耗材领用储备，防止缺货而影响麻醉工作开展。事实上，在2019年2月的耗材领用过多，造成成本核算收支不平衡，而2019年11月因耗材不足而临时加领了数次耗材。值得注意的是, 2020年的实际耗材领用支出与预测值出现了较大的偏差，这可能是突发事件新型冠状病毒肺炎疫情对预测模型的扰动，随着疫情的控制，预测能力逐渐恢复。
通过验证表明, ARIMA模型在本院麻醉科耗材领用支出方面取得了较好的预测效果。医院根据预测值合理制订采购计划，有效调控耗材的储备与采购计划。经过一段时间的试用，本院将逐步推广该模型至其他科室甚至其他医院。该模型的应用对于医院管理者而言，可以根据预测值进行耗材成本核算，为科室预算审批提供可靠依据[20]; 对于生产商和供应商而言，可以根据预测值制订更加合理的生产和备货计划，不仅可以降低库存积压成本，还可以减少紧急备货造成的额外生产成本，从而有效提高医用耗材供应链的管理水平[21]。
-
表 1 ARIMA模型极大似然方法检验和AIC
ARIMA模型 ma s. e. sma s. e log likelihood AIC ARIMA(0, 1, 1)(0, 0, 1)[12] -0.811 2 0.062 7 0.335 7 0.146 6 -27.08 60.17 ARIMA(1, 1, 0)(1, 0, 0)[12] -0.641 8 0.094 3 0.200 2 0.200 2 -30.26 66.53 ARIMA(0, 1, 1)(1, 0, 1)[12] -0.806 7 0.063 6 0.530 5 0.374 1 -26.94 61.88 ARIMA(1, 1, 1)(0, 0, 1)[12] -0.747 4 0.106 9 0.361 2 0.147 4 -26.18 60.36 ARIMA(0, 1, 2)(0, 0, 1)[12] -0.912 8 0.116 1 0.354 5 0.146 6 -26.45 60.90 
下载: 导出CSV
-
[1] SCHWINGSHACKL A, ANAND K J S. Editorial: work-life balance: essential or ephemeral[J]. Front Pediatr, 2017, 5: 108. doi: 10.3389/fped.2017.00108
[2] DESAI V, CHAN P H, PRENTICE H A, et al. Is anesthesia technique associated with a higher risk of mortality or complications within 90 days of surgery for geriatric patients with hip fractures[J]. Clin Orthop Relat Res, 2018, 476(6): 1178-1188. doi: 10.1007/s11999.0000000000000147
[3] DONNELLY G T, FORESTER L T, DONNELLY L F. Reliable and efficient supply chain management in radiology: implementation of a two-Bin demand-flow system[J]. J Am Coll Radiol, 2016, 13(4): 426-428. doi: 10.1016/j.jacr.2015.09.006
[4] GAO J Q, LI J Y, WANG M Q. Time series analysis of cumulative incidences of typhoid and paratyphoid fevers in China using both Grey and SARIMA models[J]. PLoS One, 2020, 15(10): e0241217. doi: 10.1371/journal.pone.0241217
[5] KATRIS C. A time series-based statistical approach for outbreak spread forecasting: Application of COVID-19 in Greece[J]. Expert Syst Appl, 2021, 166: 114077. doi: 10.1016/j.eswa.2020.114077
[6] ADEYINKA D A, MUHAJARINE N. Time series prediction of under-five mortality rates for Nigeria: comparative analysis of artificial neural networks, Holt-Winters exponential smoothing and autoregressive integrated moving average models[J]. BMC Med Res Methodol, 2020, 20(1): 292. doi: 10.1186/s12874-020-01159-9
[7] WEI W D, JIANG J J, LIANG H, et al. Application of a combined model with autoregressive integrated moving average (ARIMA) and generalized regression neural network (GRNN) in forecasting hepatitis incidence in Heng County, China[J]. PLoS One, 2016, 11(6): e0156768. doi: 10.1371/journal.pone.0156768
[8] RUBAIHAYO J, TUMWESIGYE N M, KONDE-LULE J, et al. Forecast analysis of any opportunistic infection among HIV positive individuals on antiretroviral therapy in Uganda[J]. BMC Public Health, 2016, 16(1): 766. doi: 10.1186/s12889-016-3455-5
[9] LUO L, LUO L, ZHANG X L, et al. Hospital daily outpatient visits forecasting using a combinatorial model based on ARIMA and SES models[J]. BMC Health Serv Res, 2017, 17(1): 469. doi: 10.1186/s12913-017-2407-9
[10] PACKARD G C. Misconceptions about logarithmic transformation and the traditional allometric method[J]. Zoology (Jena), 2017, 123: 115-120. doi: 10.1016/j.zool.2017.07.005
[11] WANG Y B, XU C J, ZHANG S K, et al. Temporal trends analysis of tuberculosis morbidity in mainland China from 1997 to 2025 using a new SARIMA-NARNNX hybrid model[J]. BMJ Open, 2019, 9(7): e024409. doi: 10.1136/bmjopen-2018-024409
[12] ANWAR M Y, LEWNARD J A, PARIKH S, et al. Time series analysis of malaria in Afghanistan: using ARIMA models to predict future trends in incidence[J]. Malar J, 2016, 15(1): 566. doi: 10.1186/s12936-016-1602-1
[13] GARLICH J M, PUJARI A, DEBBI E M, et al. Time to block: early regional anesthesia improves pain control in geriatric hip fractures[J]. J Bone Jo Surg Am Vol, 2020, 102(10): 866-872. doi: 10.2106/JBJS.19.01148
[14] LIAO Z Y, ZHANG X N, ZHANG Y H, et al. Seasonality and trend forecasting of tuberculosis incidence in Chongqing, China[J]. Interdiscip Sci, 2019, 11(1): 77-85. doi: 10.1007/s12539-019-00318-x
[15] FLEUREN L M, KLAUSCH T L T, ZWAGER C L, et al. Machine learning for the prediction of Sepsis: a systematic review and meta-analysis of diagnostic test accuracy[J]. Intensive Care Med, 2020, 46(3): 383-400. doi: 10.1007/s00134-019-05872-y
[16] BUZA K, PE?KA L, KOLLER J. Modified linear regression predicts drug-target interactions accurately[J]. PLoS One, 2020, 15(4): e0230726. doi: 10.1371/journal.pone.0230726
[17] KRIEGESKORTE N, GOLAN T. Neural network models and deep learning[J]. Curr Biol, 2019, 29(7): R231-R236. doi: 10.1016/j.cub.2019.02.034
[18] GARCIA T P, MA Y. Simultaneous treatment of unspecified heteroskedastic model error distribution and mismeasured covariates for restricted moment models[J]. J Econom, 2017, 200(2): 194-206. doi: 10.1016/j.jeconom.2017.06.005
[19] ALIM M, YE G H, GUAN P, et al. Comparison of ARIMA model and XGBoost model for prediction of human brucellosis in mainland China: a time-series study[J]. BMJ Open, 2020, 10(12): e039676. doi: 10.1136/bmjopen-2020-039676
[20] MIYAHIRA A, TADA K, ISHIMA M, et al. A trial of nursing cost accounting using nursing practice data on a hospital information system[J]. Stud Health Technol Inform, 2015, 216: 944.
[21] LIU T Z, SHEN A Z, HU X J, et al. SPD-based logistics management model of medical consumables in hospitals[J]. Iran J Public Health, 2016, 45(10): 1288-1299. http://pdfs.semanticscholar.org/8d42/e79e83d4f6c3bce9b434660b573f36fde0ee.pdf
-
期刊类型引用(1)
1. 李君，曹良海. 基于R语言时间序列的ARIMA模型预测某三甲综合医院人均月住院费用和住院日的研究. 中国卫生产业. 2024(11): 220-224 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 368
- HTML全文浏览量: 241
- PDF下载量: 9
- 被引次数: 2
苏公网安备 32100302010246号